Kampung Warna-Warni (Village Of Color)

Researchers can identify you by your brain waves with 100 percent accuracy

Your responses to certain stimuli – foods, celebrities, words – might seem trivial, but they say a lot about you. In fact (with the proper clearance), these responses could gain you access into restricted areas of the Pentagon.

A team of researchers at Binghamton University, led by Assistant Professor of Psychology Sarah Laszlo and Assistant Professor of Electrical and Computer Engineering Zhanpeng Jin, recorded the brain activity of 50 people wearing an electroencephalogram headset while they looked at a series of 500 images designed specifically to elicit unique responses from person to person – e.g., a slice of pizza, a boat, Anne Hathaway, the word “conundrum.” They found that participants’ brains reacted differently to each image, enough that a computer system was able to identify each volunteer’s “brainprint” with 100 percent accuracy.

“When you take hundreds of these images, where every person is going to feel differently about each individual one, then you can be really accurate in identifying which person it was who looked at them just by their brain activity,” said Laszlo.

In their original study, titled “Brainprint,” published in 2015 in

Neurocomputing

, the research team was able to identify one person out of a group of 32 by that person’s responses, with only 97 percent accuracy, and that study only incorporated words, not images

Maria V. Ruiz-Blondet, Zhanpeng Jin, Sarah Laszlo. CEREBRE: A Novel Method for Very High Accuracy Event-Related Potential Biometric Identification. IEEE Transactions on Information Forensics and Security, 2016; 11 (7): 1618 DOI: 10.1109/TIFS.2016.2543524

Woman wearing an EEG headset.Credit: Jonathan Cohen/Binghamton University

The Graduate, 1967.

Book Lovers Day - Free Aeronautics e-Books from NASA

Quieting the Boom

The Shaped Sonic Boom Demonstrator and the Quest for Quiet Supersonic Flight.

Download it HERE

Elegance in Flight

A comprehensive History of the F-16XL Experimental Prototype and its Role in our Flight Research. 

Download it HERE

Probing the Sky

Selected National Advisory Committee for Aeronautics (NACA) Research Airplanes and Their Contributions to Flight.

Download it HERE

Cave of the Winds

The huge Langley Full-Scale Tunnel building dominated the skyline of Langley Air Force Base for 81 years (1930–2011). Explore how the results of critical tests conducted within its massive test section contributed to many of the Nation’s most important aeronautics and space programs.

Download it HERE

A New Twist in Flight Research

A New Twist in Flight Research describes the origins and design development of aeroelastic wing technology, its application to research aircraft, the flight-test program, and follow-on research and future applications.

Download it HERE

Sweeping Forward

Developing & Flight Testing the Grumman X-29A Forward Swept Wing Research Aircraft.

Download it HERE

Thinking Obliquely

Robert T. Jones, the Oblique Wing, our AD-1 Demonstrator, and its Legacy.

Download it HERE

The Apollo of Aeronautics

The fuel crisis of the 1970s threatened not only the airline industry but also the future of American prosperity itself. It also served as the genesis of technological ingenuity and innovation from a group of scientists and engineers at NASA, who initiated planning exercises to explore new fuel-saving technologies.

Download it HERE

X-15: Extending the Frontiers of Flight

X-15: Extending the Frontiers of Flight describes the genesis of the program, the design and construction of the aircraft, years of research flights and the experiments that flew aboard them.

Download it HERE

Ikhana

Delve into the story of the Ikhana, a remotely piloted vehicle used by NASA researchers to conduct Earth science research, which became an unexpected flying and imaging helper to emergency workers battling California wildfires.

Download it HERE

NASA’s Contributions to Aeronautics, Volume 1

This first volume in a two-volume set includes case studies and essays on NACA-NASA research for contributions such as high-speed wing design, the area rule, rotary-wing aerodynamics research, sonic boom mitigation, hypersonic design, computational fluid dynamics, electronic flight control and environmentally friendly aircraft technology.

Download it HERE

NASA’s Contributions to Aeronautics, Volume 2

Continue your journey into the world  of NASA’s Contributions to Aeronautics with case studies and essays on NACA-NASA research for contributions including wind shear and lightning research, flight operations, human factors, wind tunnels, composite structures, general aviation aircraft safety, supersonic cruise aircraft research and atmospheric icing.

Download it HERE

Interested in other free e-books on topics from space, science, research and more? Discover the other e-books HERE.

Make sure to follow us on Tumblr for your regular dose of space: http://nasa.tumblr.com

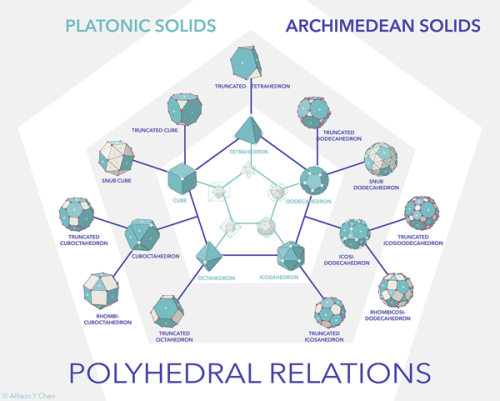
Platonic solid: In Euclidean geometry, a Platonic solid is a regular, convex polyhedron with congruent faces of regular polygons and the same number of faces meeting at each vertex. Five solids meet those criteria, and each is named after its number of faces.

An Archimedean solid is a highly symmetric, semi-regular convex polyhedron composed of two or more types of regular polygons meeting in identical vertices . They are distinct from the Platonic soilds, which are composed of only one type of polygon meeting in identical vertices, and from the Johnson solids, whose regular polygonal faces do not meet in identical vertices.

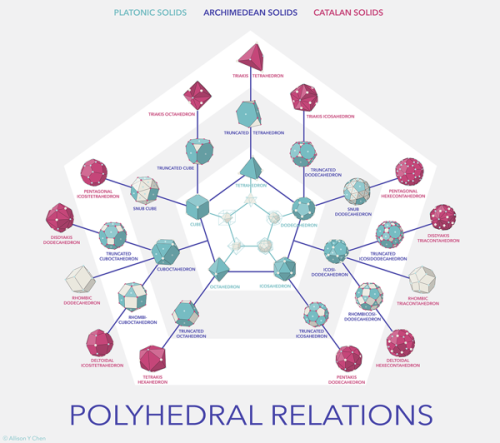
In mathematics, a Catalan solid, or Archimedean dual, is a dual polyhedron to an Archimedean soild. The Catalan solids are named for the Belgian mathematician, Eugène Catalan, who first described them in 1865.

The Catalan solids are all convex. They are face-transitive but not vertex-transitive. This is because the dual Archimedean solids are vertex-transitive and not face-transitive. Note that unlike Platonic soilds  and Archimedean soild, the faces of Catalan solids are not regular polygons. However, the vertex figures of Catalan solids are regular, and they have constant dihedral angles. Additionally, two of the Catalan solids are edge-transitive: the rhombic dodecahedron and the rhombic triacontahedron. These are the duals of the two quasi-regular Archimedean solids.

Images: Polyhedral Relations by Allison Chen on Behance.

Everyday Phenomena: The Maillard Reaction

At first glance, steak, French fries, bread, milk caramel, and soy sauce don’t have very many similarities. However, the preparation of these foods all have one thing in common: browning that occurs via the Maillard (my-YAR) reaction.

The Maillard reaction was first discovered in 1912 by Louis-Camille Maillard, and refers to a long chain of reactions that ultimately leads to browning of food. This chain typically begins with the condensation of an amine (often the amino acid lysine) with a reducing sugar (containing an aldehyde); one example of this Amadori rearrangement is shown above with lysine and glucose.

This Amadori product can react in a variety of different ways, including dehydration and deamination to produce a diverse array of molecules that give browned food a distinctive flavor; a few of these compounds are shown above. At the end of the sequence of reactions that occur during browning is a class of polymeric compounds known as melanoidins, which lend a brown color to the food.

Below about 140°C (280°F), the Maillard reaction does not proceed at an appreciable rate, although alkaline conditions (such as the lye used to make pretzels) can accelerate the process. Without this reaction, many foods we enjoy now wouldn’t be nearly as tasty!

Further Reading: Hodge, J. E., J. Agric. Food Chem. 1953, 1 (15), 928-943 (Full text)

Are Complex Numbers Really Numbers?

If you look through definitions of “number” most will say that numbers are used to represent quantities (amounts or measures). Whole numbers 0, 1, 2, 3, … are probably the first numbers that come to mind and they are often used to count things like say how may watermelons jimmy has. But when quantifying things like money, whole numbers are not always enough and so we have rational numbers (which include the whole numbers but also fractions and numbers with finite or repeating decimal expansions). Yet, sometimes even these numbers are not enough to express certain quantities. Pi, for example, is not a rational number but is certainly a number as it represents the quantity that is the ratio of a circle’s circumference to its diameter. It can be shown that the number pi has an infinite decimal expansion with no repeating patterns, and so a number like pi is called an irrational number. (Because they are silly? Although at first some thought so, the term irrational just means not rational.)  More specifically, pi is a transcendental number as it is not the root of any polynomial. (Transcendental, because they transcend the usual notion of number? Idk. Again, strange names.) So, the rational numbers were extended to the real numbers to include both rational and irrational numbers. Either way, we see that both rational and irrational numbers are truly numbers since they can be used to represent quantities.

What about complex numbers though? Are they really numbers, or do people just call them “numbers”? So, we should ask, can complex numbers represent some amount or measure of something? Can jimmy have i watermelons? No, but jimmy can’t really have pi watermelons either and pi is a number. Jimmy may have a watermelon that weighs pi pounds though (the only way to know this would be if jimmy had a scale with infinite accuracy, which, turns out, he does). Okay but can jimmy have a watermelon weighing i pounds? That doesn’t seem to make sense. To see if complex numbers can represent quantities we need to elaborate on what complex numbers are exactly.

The complex numbers are the real numbers extended to include the square root of negative 1 (i) and all its multiples. They have the form a+bi where a and b are real numbers. i is called an imaginary number (named imaginary because, i is not a real number, but this implies numbers like i are somehow not “real”, in the usual English sense of the word (are any numbers really “real”?) again, with the names). What truly makes complex numbers different than the other numbers we have discussed is that they “live” in 2 dimensions (the complex plane); complex numbers (e.g., 7+2i) have a real part (7) and an imaginary part (2i). While real numbers (which include whole, rational, and irrational numbers) “live” in one dimension (they can be found anywhere on the number line).

So, a complex number is a sort of two-dimensional quantity, it has a real measure and an imaginary measure. This makes them strange as numbers. We know 12 is bigger than 11 and that there are a bunch of numbers in-between 11 and 12, but which is bigger 2-8i or 3+i? Complex numbers cannot be compared in the same way i.e., there is no way to order complex numbers from smallest to largest.

These properties make complex numbers more abstract than typical numbers we encounter day to day. Nevertheless, “complex numbers are useful abstract quantities that can be used in calculations and result in physically meaningful solutions. However, recognition of this fact is one that took a long time for mathematicians to accept.”—Wolfram MathWorld http://mathworld.wolfram.com/ComplexNumber.html

The Roly Poly Pudding - Beatrix Potter 

First Edition - Second Printing 1908 

[5500 copies Dec. 1908]

Why do we love?

Ah, romantic love; beautiful and intoxicating, heart-breaking and soul-crushing… often all at the same time! Why do we choose to put ourselves though its emotional wringer? Does love make our lives meaningful, or is it an escape from our loneliness and suffering?  Is love a disguise for our sexual desire, or a trick of biology to make us procreate? Is it all we need? Do we need it at all?

If romantic love has a purpose, neither science nor psychology has discovered it yet – but over the course of history, some of our most respected philosophers have put forward some intriguing theories.

1. Love makes us whole, again / Plato (427—347 BCE)

The ancient Greek philosopher Plato explored the idea that we love in order to become complete. In his Symposium, he wrote about a dinner party at which Aristophanes, a comic playwright, regales the guests with the following story. Humans were once creatures with four arms, four legs, and two faces.  One day they angered the gods, and Zeus sliced them all in two. Since then, every person has been missing half of him or herself.  Love is the longing to find a soul mate who will make us feel whole again… or at least that’s what Plato believed a drunken comedian would say at a party.

2. Love tricks us into having babies / Schopenhauer (1788-1860)

Much, much later, German philosopher Arthur Schopenhauer maintained that love, based in sexual desire, was a “voluptuous illusion”.  He suggested that we love because our desires lead us to believe that another person will make us happy, but we are sorely mistaken.  Nature is tricking us into procreating and the loving fusion we seek is consummated in our children.  When our sexual desires are satisfied, we are thrown back into our tormented existences, and we succeed only in maintaining the species and perpetuating the cycle of human drudgery.  Sounds like somebody needs a hug.

3. Love is escape from our loneliness / Russell (1872-1970)

According to the Nobel Prize-winning British philosopher Bertrand Russell we love in order to quench our physical and psychological desires.  Humans are designed to procreate; but, without the ecstasy of passionate love, sex is unsatisfying.  Our fear of the cold, cruel world tempts us to build hard shells to protect and isolate ourselves.  Love’s delight, intimacy, and warmth helps us overcome our fear of the world, escape our lonely shells, and engage more abundantly in life.  Love enriches our whole being, making it the best thing in life.  

4. Love is a misleading affliction / Buddha (~6th- 4thC BCE)

Siddhartha Gautama. who became known as ‘the Buddha’, or ‘the enlightened one’, probably would have had some interesting arguments with Russell. Buddha proposed that we love because we are trying to satisfy our base desires.  Yet, our passionate cravings are defects, and attachments – even romantic love – are a great source of suffering.  Luckily, Buddha discovered the eight-fold path, a sort of program for extinguishing the fires of desire so that we can reach ‘nirvana’ – an enlightened state of peace, clarity, wisdom, and compassion.  

5. Love lets us reach beyond ourselves / Beauvoir (1908-86)

Let’s end on a slightly more positive note.  The French philosopher Simone de Beauvoir proposed that love is the desire to integrate with another and that it infuses our lives with meaning.  However, she was less concerned with why we love and more interested in how we can love better.  She saw that the problem with traditional romantic love is it can be so captivating that we are tempted to make it our only reason for being.  Yet, dependence on another to justify our existence easily leads to boredom and power games.  

To avoid this trap, Beauvoir advised loving authentically, which is more like a great friendship: lovers support each other in discovering themselves, reaching beyond themselves, and enriching their lives and the world, together.

Though we might never know why we fall in love, we can be certain that it’ll be an emotional rollercoaster ride.  It’s scary and exhilarating.  It makes us suffer and makes us soar.  Maybe we lose ourselves.  Maybe we find ourselves.  It might be heartbreaking or it might just be the best thing in life.  Will you dare to find out? 

From the TED-Ed Lesson Why do we love? A philosophical inquiry - Skye C. Cleary

Animation by Avi Ofer

New CDC Research Debunks Agency’s Assertion That Mercury in Vaccines Is Safe

The CDC study, Alkyl Mercury-Induced Toxicity: Multiple Mechanisms of Action, appeared last month in the journal, Reviews of Environmental Contamination and Toxicology. The 45-page meta-review of relevant science examines the various ways that mercury harms the human body. Its authors, John F. Risher, PhD, and Pamela Tucker, MD, are researchers in the CDC’s Division of Toxicology and Human Health Sciences, Agency for Toxic Substances and Disease Registry.

“This scientific paper is the one of most important pieces of research to come out of the CDC in a decade,” Paul Thomas, M.D., a Dartmouth-trained pediatrician who has been practicing medicine for 30 years, said. “It confirms what so many already suspected: that public health officials have been making a terrible mistake in recommending that we expose babies and pregnant women to this neurotoxin. I regret to say that I gave these shots to children. The CDC led us all to believe that it was perfectly safe.”

Among the findings of the CDC’s new study:

Methylmercury, the highly-regulated neurotoxin found in fish, and ethylmercury (found in medical products, including influenza and tetanus vaccines, ear drops and nasal sprays) are similarly toxic to humans. Methylmercury and ethylmercury share common chemical properties, and both significantly disrupt central nervous system development and function.

Thimerosal is extremely toxic at very low exposures and is more damaging than methylmercury in some studies. For example, ethylmercury is even more destructive to the mitochondria in cells than methylmercury.

The ethylmercury in thimerosal does not leave the body quickly as the CDC once claimed, but is metabolized into highly neurotoxic forms.

Top image via The Roald Dahl Museum and Story Centre

Happy Roald Dahl Day, everyone!  

Here’s a selection of some of our favorite stories about the man behind Matilda, Charlie and the Chocolate Factory, The BFG and all the other books that traumatized us so delightfully as kids (Vermicious Knids, eeeeeggghhh).

Roald Dahl Wanted His Magical ‘Matilda’ To Keep Books Alive

Roald Dahl, A Bottle Of Dreams And A 'Letter Of Note’

'Where Am I Now?’ Mara Wilson Explains What Happened When Matilda Grew Up

Roald Dahl: The Story Of The 'Storyteller’

And lest we forget – Dahl’s memoirs and fiction for adults are great too. Just don’t  give Someone Like You to a kid.

Wicked And Delicious: Devouring Roald Dahl

– Petra