Shall We Go And Eat




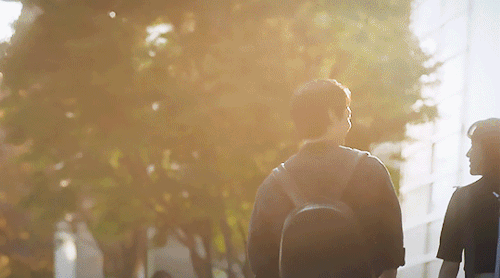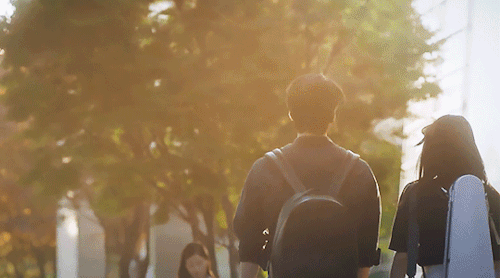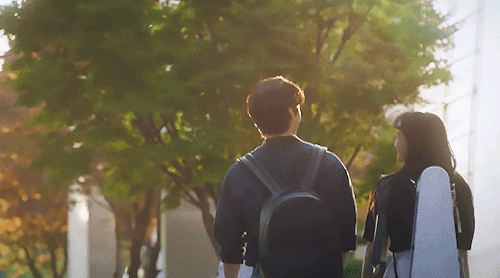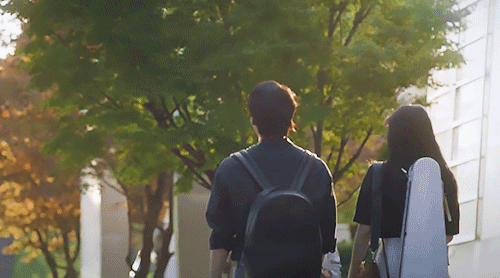
shall we go and eat
More Posts from Parkhanyoonjae and Others


You all know my love for afternoon study sessions


Photography 13/n 📷
at the University forest
17 June 2024
The calmness of the forest gives me peace of mind.



Middle Term Diaries 1/n 💊🏫
house at midnight
02 July 2024
After finishing the laboratory reports that I assigned to myself, I reviewed for my midterm exam in Medicinal Organic Chemistry even though I felt lazy to review.
![[research Life]](https://64.media.tumblr.com/cc5fd9fa42180622f007443f539d7f0b/7a4c3658168046a2-e8/s500x750/d12a486905df38a51b7ac5dbc8f7918231d8441a.jpg)
![[research Life]](https://64.media.tumblr.com/c513cdf1008e7b7afa95f9d29f745ad8/7a4c3658168046a2-7a/s500x750/57840277f47da2f6be8dbe187eae8c890d6ad34b.jpg)
[research life]
A Friday spent writing + reading 🩵📝📚










Yoon Chan-young and Bong Jae-hyun for Marie Claire Korea (May 2024)






Laboratoire 1/n 🥼
Laboratory
19 September 2023
The making of agar for the acquisition of microbiological sample 🧫🦠

Jane Austen, from a letter to her sister Cassandra Austen
![— Roland Barthes, A Lover's Discourse; Fragments [translated By Richard Howard]](https://64.media.tumblr.com/9c0bb12af24794f97eea027966789521/f13c1ff0f1b86df4-de/s500x750/e10cd8b95aeb3c5c64bc438a418d1299208825b2.jpg)
— Roland Barthes, A Lover's Discourse; Fragments [translated by Richard Howard]
Real-Life Uses of Calculus
Calculus isn’t just an abstract, ivory tower concept relegated to textbooks—it’s a powerful tool woven deeply into the fabric of our daily lives, from the precision of medical dosage to the unpredictability of the stock market.
1. Medicine: Optimizing Drug Dosage
Calculus plays a key role in pharmacokinetics, the branch of science that deals with the absorption, distribution, metabolism, and excretion of drugs in the body. When doctors prescribe medication, they need to ensure that drug levels remain within therapeutic bounds, not too high to cause toxicity and not too low to be ineffective. This is where differential equations, a core part of calculus, come into play. The rate of change of drug concentration over time is modeled with calculus to determine optimal dosage and scheduling for sustained, effective drug levels.
Take antibiotics, for example: they must be administered at specific intervals to maintain an effective concentration in the bloodstream while preventing bacterial resistance. Calculus allows for the continuous monitoring of drug levels and the adjustment of dosages based on individual metabolism rates, ensuring maximum therapeutic benefit.
2. Physics and Engineering: Motion and Forces
In classical mechanics, calculus is used to describe motion. Newton's laws of motion and universal gravitation are based on derivatives and integrals, the foundational elements of calculus. The change in velocity (acceleration) is the derivative of position with respect to time, while the area under the velocity-time graph gives us the distance traveled.
For instance, when designing cars, engineers use calculus to model the forces acting on the vehicle, such as friction, air resistance, and engine power. Calculus helps optimize everything from fuel efficiency to safety features, ensuring that a car can handle various conditions without exceeding performance thresholds.
3. Economics and Finance: Predicting Stock Market Trends
In economics, calculus is used to understand and predict market behavior. The concept of marginal analysis—examining the effects of small changes in variables—relies heavily on calculus. For example, marginal cost is the derivative of total cost with respect to quantity, and marginal revenue is the derivative of total revenue with respect to the quantity of goods sold.
In the stock market, calculus is utilized in quantitative finance to model stock prices using stochastic differential equations. Techniques like Black-Scholes for options pricing rely on calculus to determine the fair price of financial derivatives by analyzing how small fluctuations in stock prices impact their expected value. The concept of risk management—how much risk is worth taking for a given return—also uses derivatives to evaluate the rate of change of potential outcomes over time.
4. Environmental Science: Climate Modeling
Climate change models are inherently tied to calculus. Calculus is used to model the flow of energy through the Earth's atmosphere, oceans, and land, and how this energy affects global temperatures. The change in temperature over time is governed by differential equations, accounting for factors like greenhouse gas emissions, solar radiation, and ocean currents. As a result, climate scientists use calculus to predict future climate scenarios under various emission levels, helping inform policy decisions on global warming and sustainability.
5. Computer Science and Machine Learning: Optimization Algorithms
In machine learning, algorithms are designed to optimize a given function—whether it's minimizing the error in predictions or maximizing efficiency in a task. These algorithms often rely on derivatives to find the minimum or maximum of a function. For example, gradient descent, a popular optimization algorithm, uses the derivative of a function to iteratively adjust parameters and reach the optimal solution.
In computer graphics, calculus is essential for creating smooth curves and realistic animations. The mathematical process of curvature, which is the rate of change of direction along a curve, is vital for rendering images in 3D modeling and augmented reality.
6. Astronomy and Space Exploration: Orbital Mechanics
In space travel, calculus is crucial in calculating orbits, trajectories, and spaceship velocity. The path a spacecraft takes through space is influenced by gravitational forces, which can be modeled using calculus. For example, NASA’s mission to Mars relied on calculus to calculate the optimal launch window by accounting for the positions and motions of both Earth and Mars, ensuring the spacecraft would reach its destination efficiently.










Buhay Colegio - Primer año 🏫
LPU - Cavite (General Trias, Cavite)
2019-2020
Seeing these pictures in my gallery gives me a lot of wonderful memories I had when I was in first year (4-5 years ago). My classmates were already graduated in college and some of them passed the PhLE last 23 April 2024. I am proud of them 🥹😭💗 I miss you so much fellas
-
 niallslilacpants reblogged this · 4 months ago
niallslilacpants reblogged this · 4 months ago -
 try-again-bissh liked this · 6 months ago
try-again-bissh liked this · 6 months ago -
 parkhanyoonjae reblogged this · 1 year ago
parkhanyoonjae reblogged this · 1 year ago -
 parkhanyoonjae liked this · 1 year ago
parkhanyoonjae liked this · 1 year ago -
 rizblogs liked this · 1 year ago
rizblogs liked this · 1 year ago -
 shayahoo reblogged this · 1 year ago
shayahoo reblogged this · 1 year ago -
 mapommerouge liked this · 2 years ago
mapommerouge liked this · 2 years ago -
 oatmealnebraska liked this · 2 years ago
oatmealnebraska liked this · 2 years ago -
 jennifercarrillo26 liked this · 2 years ago
jennifercarrillo26 liked this · 2 years ago -
 nap-hime reblogged this · 2 years ago
nap-hime reblogged this · 2 years ago -
 seekers-who-are-lovers liked this · 2 years ago
seekers-who-are-lovers liked this · 2 years ago -
 wannabeajedi liked this · 2 years ago
wannabeajedi liked this · 2 years ago -
 leej0ngsuk reblogged this · 2 years ago
leej0ngsuk reblogged this · 2 years ago -
 dearestnico liked this · 2 years ago
dearestnico liked this · 2 years ago -
 mjcopycat liked this · 2 years ago
mjcopycat liked this · 2 years ago -
 glass-of-memories liked this · 2 years ago
glass-of-memories liked this · 2 years ago -
 willievermakeithome liked this · 2 years ago
willievermakeithome liked this · 2 years ago -
 elamora liked this · 2 years ago
elamora liked this · 2 years ago -
 meetmebehndthemalll reblogged this · 2 years ago
meetmebehndthemalll reblogged this · 2 years ago -
 ehohaeh reblogged this · 2 years ago
ehohaeh reblogged this · 2 years ago -
 mypassengerseat liked this · 3 years ago
mypassengerseat liked this · 3 years ago -
 measuringcups liked this · 3 years ago
measuringcups liked this · 3 years ago -
 anchovious-berrie liked this · 3 years ago
anchovious-berrie liked this · 3 years ago -
 anime90hpdreamer liked this · 3 years ago
anime90hpdreamer liked this · 3 years ago -
 stoicandbreathing reblogged this · 3 years ago
stoicandbreathing reblogged this · 3 years ago -
 stoicandbreathing liked this · 3 years ago
stoicandbreathing liked this · 3 years ago -
 korean-dramaland reblogged this · 3 years ago
korean-dramaland reblogged this · 3 years ago -
 winterwitch107th liked this · 3 years ago
winterwitch107th liked this · 3 years ago -
 toddbl4ck reblogged this · 3 years ago
toddbl4ck reblogged this · 3 years ago -
 ghostlysea liked this · 3 years ago
ghostlysea liked this · 3 years ago -
 sarahbasques liked this · 3 years ago
sarahbasques liked this · 3 years ago -
 tierdeyesarethedeathinme liked this · 3 years ago
tierdeyesarethedeathinme liked this · 3 years ago -
 infernalhanbin reblogged this · 3 years ago
infernalhanbin reblogged this · 3 years ago -
 infernalhanbin liked this · 3 years ago
infernalhanbin liked this · 3 years ago -
 inquisitivemind-indolentsoul liked this · 3 years ago
inquisitivemind-indolentsoul liked this · 3 years ago -
 island-stars liked this · 3 years ago
island-stars liked this · 3 years ago -
 narsicen liked this · 3 years ago
narsicen liked this · 3 years ago -
 avatarslovemp3 liked this · 3 years ago
avatarslovemp3 liked this · 3 years ago -
 lahmatom liked this · 3 years ago
lahmatom liked this · 3 years ago -
 isfjwptsd liked this · 3 years ago
isfjwptsd liked this · 3 years ago -
 randomgirlrambles liked this · 3 years ago
randomgirlrambles liked this · 3 years ago -
 itsodelialove liked this · 3 years ago
itsodelialove liked this · 3 years ago -
 nocassandra reblogged this · 3 years ago
nocassandra reblogged this · 3 years ago -
 villainaesthtic liked this · 3 years ago
villainaesthtic liked this · 3 years ago -
 lilacskiesonyourmind reblogged this · 3 years ago
lilacskiesonyourmind reblogged this · 3 years ago -
 lilacskiesonyourmind liked this · 3 years ago
lilacskiesonyourmind liked this · 3 years ago -
 fangirl-bookaholic liked this · 3 years ago
fangirl-bookaholic liked this · 3 years ago
